Have you ever wondered how the laws of physics come to be? It turns out that the answer is not as straightforward as we thought. In the field of condensed matter physics, scientists study how matter and forces can emerge from seemingly unrelated phenomena. But it doesn’t stop there - spacetime and even gravity can also emerge from complex networks. And here’s a mind-bending idea: physics theories themselves might be emergent phenomena that arise from collective neural activations in the brains of physicists! It’s a fascinating concept that begs the question: how do these ideas come to life in our minds? As scientists, we strive to unravel the universal principles of emergent intelligence in complex networks, and it’s an exciting journey that we’re still on.

While we are still far from a complete understanding of intelligence, recent developments in machine learning have allowed us to take a step in that direction. Specifically, we are interested in whether artificial neural networks can be used to discover physical concepts and laws from experimental data.

To illustrate this concept, let’s consider the case of quantum mechanics. Imagine if quantum mechanics had not yet been formulated, but physicists knew how to perform cold atom experiments to collect density distributions of Bose-Einstein condensate (BEC) in potential traps of different shapes. Could quantum mechanics be discovered as the most natural theory to explain the experimental data without any prior human bias? Or would the machine come up with an alternative form of quantum mechanics?

In our recent work arXiv:1901.11103, we show how a machine learning algorithm can discover quantum mechanics by learning to predict the BEC density given the potential profile. Remarkably, the machine is only exposed to the data of potentials and densities, yet the quantum wave function can emerge as latent variables in the neural network.

We are inspired by the development of machine translation, which is trained to map sequences of words from one language to another. The machine translator can develop a semantic space in its hidden layers, which holds the intrinsic representation of words or phrases that are universal to all languages. By analyzing the structure of the semantic space, we can gain understanding about the relations among words as perceived by the translator.

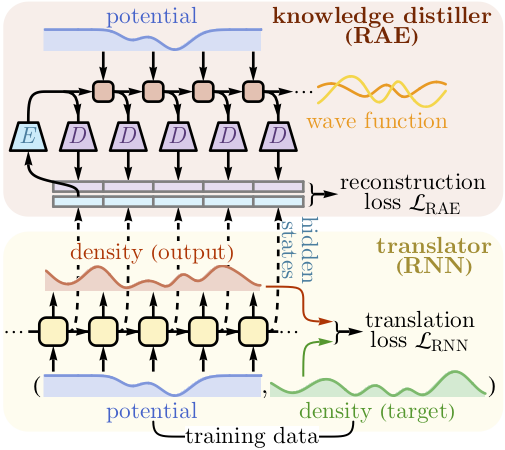
To apply this idea to the problem at hand, we treat the potential-to-density mapping as an example of sequence-to-sequence mapping that can be handled by the machine translation approach, such as the recurrent neural network. We train a recurrent neural network to translate the potential profile to the density profile along a one-dimensional trap. By learning to perform this translation, the machine gains intuitions about the underlying physics.

To extract what the machine translator has learned, we design a higher-level machine, called a knowledge distiller, to learn from the neural activations (hidden states) of the lower-level translator. The knowledge distiller is an auto-encoder incorporated in another recurrent neural network structure. Its task is to compress the hidden states generated by the translator at each step as much as possible without losing the prediction power to reconstruct subsequent hidden states. This allows the knowledge distiller to identify the essential variables.

Our study shows that the reconstruction loss of the knowledge distiller only increases abruptly when its latent space dimension is reduced below two. This implies that at least two real variables are required to describe the behavior of the potential-to-density translator. When we plot these two variables, they correspond to the real and imaginary parts of the quantum wave function (up to basis freedom). Further inspection of the update rules for these variables shows that they are governed by a recurrent relation that precisely matches the discrete version of the Schrödinger equation. Thus, knowledge about quantum mechanics emerges in the neural network.

Furthermore, if we relax the information bottleneck of the knowledge distiller, alternative forms of quantum mechanics, such as density functional theory, could also emerge, but it requires at least three real variables to describe. It is reassuring to know that the current formulation of quantum mechanics, in terms of the wave function and Schrödinger equation, is indeed the most parsimonious theory among all alternative theories of quantum mechanics that have been discovered in our neural network.