Have you ever noticed a pattern in your carpet or tiles that creates a larger, intricate design? That’s called a Moire pattern, and it’s created when two periodic lattices lie on top of each other with a relative twist or a mismatched lattice constant. In the world of physics, this pattern can emerge in a fascinating way when stacking 2D materials like graphene, hexagonal boron nitride (hBN), molybdenum disulfide, and many others. By doing so, we can create a Moire superlattice, which is essentially a larger lattice that forms as a result of the interference between the two smaller lattices.

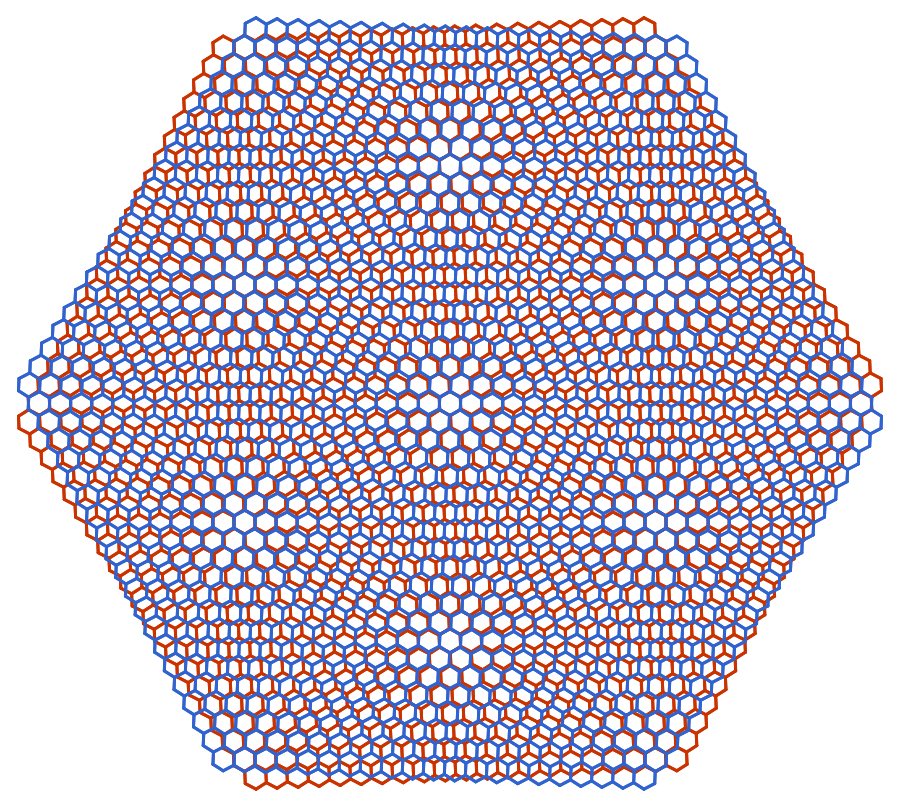
Why is this so exciting? Well, it turns out that new physics can emerge on Moire superlattices, including Mott insulators, unconventional superconductors, and even new topological phases. How is this possible? One way to understand it is to consider that as the lattice length scale increases, the electronic matter wave also propagates at a longer wavelength on the lattice, which corresponds to a lower momentum. Since the kinetic energy of the electron positively correlates with its momentum, the reduced momentum on the superlattice implies a reduced kinetic energy. This makes the interaction energy relatively more important compared to the kinetic energy, resulting in the enhanced interaction effect among the electrons.

In fact, band structure calculations reveal that at certain twist angles (known as the magic angle), the electronic band near the Fermi energy can become very flat. This opens up a platform for strongly correlated quantum many-body physics to take place. Typically, there are two approaches to handle these correlated electronic systems: one is the weak coupling approach that starts with the electronic band structure and adds in interaction perturbatively, while the other is the strong coupling approach that starts with the clusters of electrons with strong local interaction and tries to connect them together through virtual tunneling processes.

In my recent work (arXiv:1805.06867) with Ashvin Vishwanath, we propose a low-energy effective theory for twisted bilayer graphene and follow the weak coupling approach to analyze the leading ordering instability, including the possible pairing symmetries. My group is also actively exploring the strong coupling approach to gain a more comprehensive understanding of the correlated physics in these Moire superlattice systems. So the next time you see a Moire pattern in your surroundings, just remember that this simple phenomenon can lead to exciting discoveries in the world of physics.