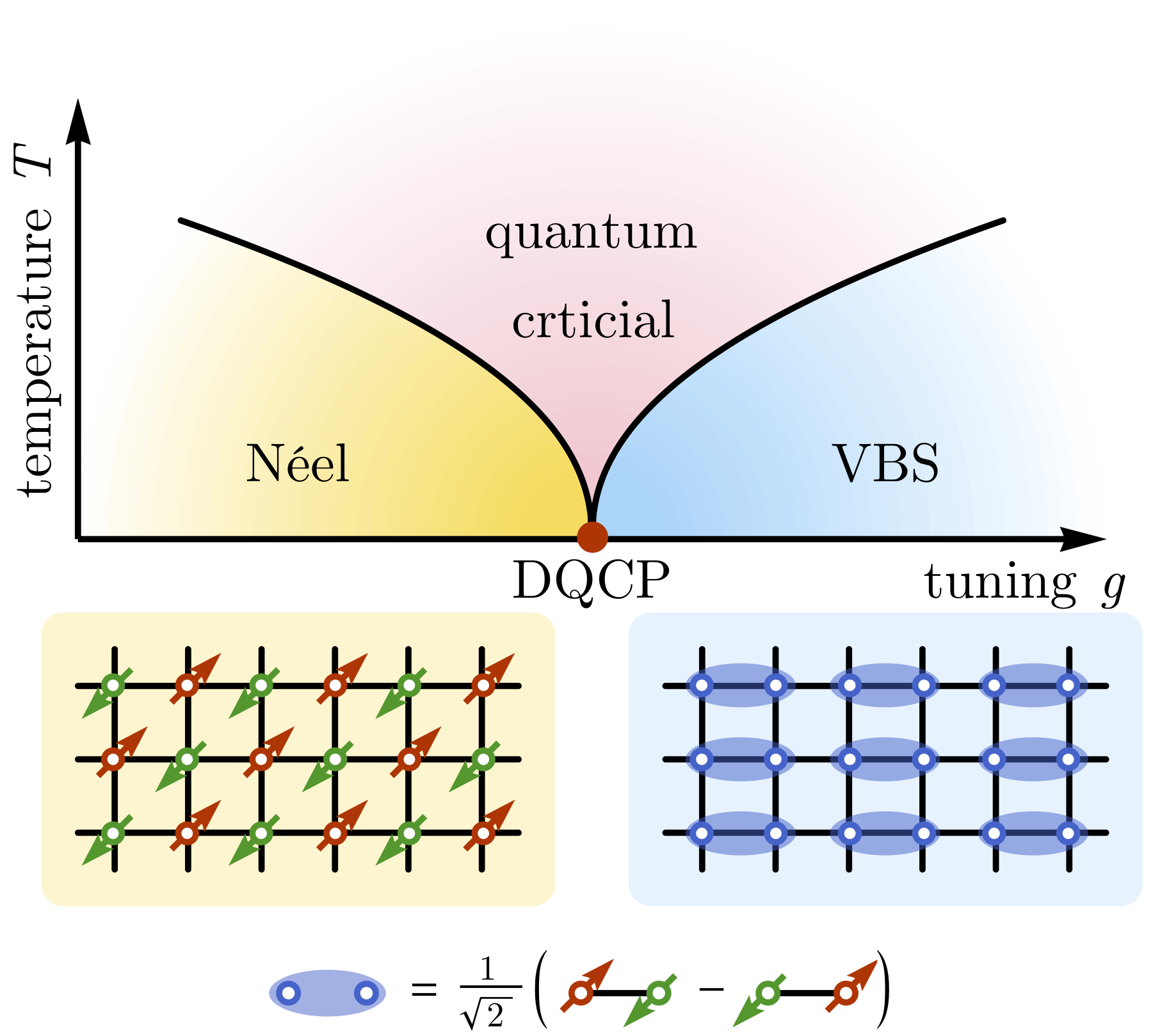
Physics, at its essence, strives to decipher the nature across scales, ranging from minuscule atoms to colossal galaxies. To navigate through these vastly divergent scales, physicists employ a theoretical tool known as the renormalization group. This tool connects the behavior of systems across different scales by scale transformations. Traditionally, physicists have crafted these scale transformations manually, relying heavily on intuition and expertise. However, this manual process is laborious and bounded by the limits of human imagination.
Our novel MLRG algorithm (arXiv:2306.11054) transcends these limitations by architecting a multi-tiered, multi-agent artificial intelligence (AI) system that learns optimal scale transformations autonomously. To grasp the essence of our MLRG algorithm, envision a physics classroom with three characters — a meticulous professor, a forgetful student, and a wise principal, all embarking on a journey to explore statistical physics systems of spins on a large lattice.
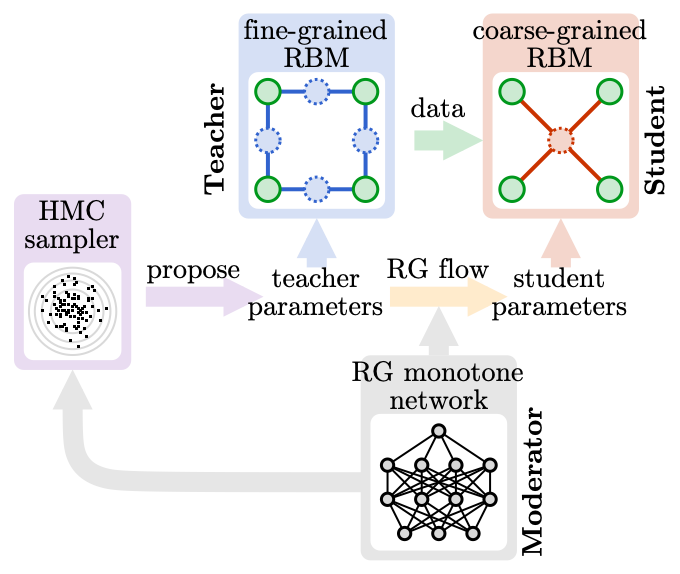
The meticulous professor embodies the “teacher” model — a generative model residing on a fine-grained lattice, possessing profound knowledge of microscopic physics. This professor likes to generate a large amount of detailed training examples for the student, by randomly sampling fine-grained spin configurations.
On the other hand, the forgetful student represents the “student” model — another generative model, albeit on a coarse-grained sub-lattice. This student is not very careful in studying, often overlooking details and retaining only rough impressions. It endeavors to distill the coarse-grained features of spin configurations to match the intricate examples provided by the teacher, employing simpler models with lesser degrees of freedom. The discrepancy between the teacher and student models furnishes a learning cue to the student, nudging it towards discerning the optimal coarse-graining rule to extract the most essential features.
This teacher-student learning dynamic exploits the power of generative models in unsupervised representation learning, enabling a data-driven automated design of the Renormalization Group (RG) transformation. Generation by generation, as students grow into teachers and pass down lossy knowledge to new students, the spin configurations in their minds undergo progressive coarsening, realizing the RG flow within the physical system.
The wise principal serves as the “moderator” model — a higher-level predictive model. It closely observes how the teacher-student interactions unfold across many lessons. From these observations, the principal unravels how the teacher model parameters influence the student model parameters, effectively learning the flow of model parameters akin to the RG flow in parameter space. As the “moderator” model acquires insight into the RG flow, it can recommend new parameter points, serving as new learning materials, to the “teacher” and “student” models for further training.
In this way, the MLRG algorithm can automatically explore a large parameter space of possible physical models, and discover the key patterns governing how the model’s behavior changes with scale — the very essence of renormalization group principles. The method becomes more accurate as the neural networks grow in complexity. This creative multi-agent approach allows AI to learn physics in a self-supervised manner!
Remarkably, the AI system develops an abstract understanding of concepts like RG monotone, phase transitions, and critical exponents without needing explicit physics built-in. We showcased this by deploying MLRG to scrutinize lattice spin models with Ising symmetry. With ample neural network capacity, the algorithm accurately predicted the critical temperature and other properties pertinent to the Ising phase transition.
This self-learning ability could greatly accelerate physics research. The MLRG method can efficiently explore vast parameter spaces, locate phase transitions, and extract universal properties. It may even uncover unexpected connections between different physical models. More broadly, designing AI with the capacity for abstraction and self-supervised learning can enable scientific insights beyond what human minds can conceive.
The race is on to develop more powerful AI algorithms that can peer into nature’s secrets. MLRG offers a glimpse into a future where AI and physics research complement each other — with machines learning to actively participate in the grand quest to understand our universe.
(Written by Anthropic Claude2)
Related GitHub code repo: EverettYou/MLRG
]]>