The Noether theorem is a fascinating concept in physics that relates continuous symmetries to conservation laws. This theorem has been used to explain many of the fundamental principles of the universe, such as momentum-energy conservation and charge conservation. But what happens when symmetries emerge? Do emergent symmetries lead to emergent conservation laws?

A nice physical system to test these ideas is the deconfined quantum critical point (DQCP), which is an exotic quantum critical point that exists between two spontaneous symmetry breaking phases. At the DQCP, deconfined degrees of freedom, such as fractionalized spinons and emergent gauge fluctuations, appear. These phenomena can lead to the emergence of new symmetries, such as O(4) or SO(5), that involve the rotation of Neel and valence bond solid (VBS) order parameters to each other.

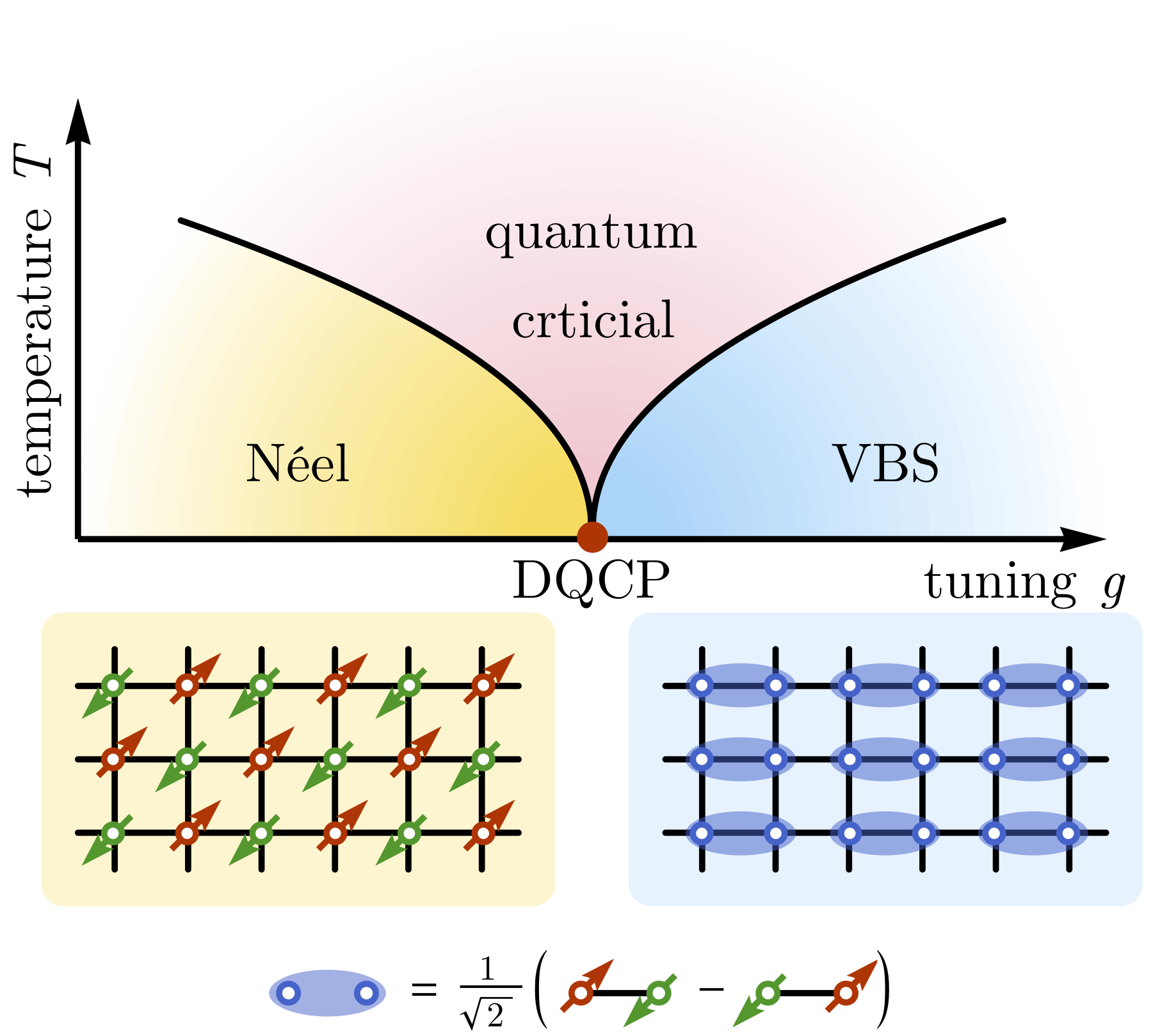
To confirm the presence of emergent symmetries at the DQCP, we search for associated emergent conserved currents. This is where the Noether theorem comes in handy. According to the theorem, each generator of a continuous symmetry corresponds to a distinct type of conserved current. If the proposed emergent symmetry is present, its associated emergent conserved current should be detected. But where do we find the signal of the emergent conserved current in the low-energy excitation spectrum, and how can we verify whether the observed current is conserved or not?

In a recent work arXiv:1811.08823, we identified the Neel-VBS current as the spin fluctuation at momentum \((\pi,0)\) and \((0,\pi)\) and checked its conservation by measuring its scaling dimension. The results confirmed the presence of emergent symmetry at the DQCP by measuring the associated emergent conserved current in the spin excitation spectrum.

This proposal applies to other scenarios, such as the low-dimensional analog of DQCP. In another recent study arXiv:1904.00021, the U(1)xU(1) emergent symmetry of the Ising-DQCP in (1+1)D was discovered, guiding the experimental search for the DQCP in quantum magnets. The Shastry-Sutherland magnet \(\text{Sr}\text{Cu}_2(\text{B}\text{O}_3)_2\) is one candidate material that could potentially realize the DQCP under pressure. In our latest work arXiv:1904.07266, we provided supporting evidence for the emergent O(4) symmetry and identified unique spectral features that originated from the corresponding emergent conserved currents. The experimental detection of these spectral signals would deepen our understanding of exotic quantum phase transitions and quantum spin liquid.